Difference between revisions of "Golygons"

 
(12 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 +
{{in progress}}
 +
{{italian}}
 +
 +
[[File:Goly1.png|thumb|70px|right|Golygons of first (N=8) and second (N=16) order.]]
 +
 
MANCA UN SACCO DI ROBA ED E' TUTTO UN DISORDINE SIGNORA MIA
 
MANCA UN SACCO DI ROBA ED E' TUTTO UN DISORDINE SIGNORA MIA
  
Line 4: Line 9:
 
<br>
 
<br>
 
dato un generico goligono di N lati:<br>
 
dato un generico goligono di N lati:<br>
−
- la sommatoria dei lati dispari sarà N<sup>2</sup>/4<br>
+
- la sommatoria dei lati dispari sarà <m>\frac{N^2}{4}</m><br>
−
- la sommatoria dei lati pari sarà N<sup>2</sup>/4 + N/2<br>
+
- la sommatoria dei lati pari sarà <m>\frac{N^2}{4} + \frac{N}{2}</m>
 
<br>
 
<br>
 
affinché il goligono sia chiuso:<br>
 
affinché il goligono sia chiuso:<br>
−
- i lati dispari che vanno a dx devono avere sommatoria uguale a quelli che vanno a sinistra, pari a N<sup>2</sup>/8<br>
+
- i lati dispari che vanno a dx devono avere sommatoria uguale a quelli che vanno a sinistra, pari a <m>\frac{N^2}{8}</m><br>
−
- i lati pari che vanno in alto devono avere sommatoria uguale a quelli che vanno in basso, pari a N<sup>2</sup>/8 + N/4
+
- i lati pari che vanno in alto devono avere sommatoria uguale a quelli che vanno in basso, pari a <m>\frac{N^2}{8}+\frac{N}{4}</m>
  
−
===Dimostrazione che i goligoni devono necessariamente avere numero di lati multiplo di 8===
+
==Dimostrazione che i goligoni devono necessariamente avere numero di lati multiplo di 8==
 
- i lati pari che vanno in alto devono avere sommatoria uguale a quelli che vanno in basso, pari a N^2/8 + N/4</blockquote>ipotizziamo per assurdo che N sia multiplo di 4 ma non di 8, allora può essere scritto nella forma N = 4A dove A è un intero dispari. <br>
 
- i lati pari che vanno in alto devono avere sommatoria uguale a quelli che vanno in basso, pari a N^2/8 + N/4</blockquote>ipotizziamo per assurdo che N sia multiplo di 4 ma non di 8, allora può essere scritto nella forma N = 4A dove A è un intero dispari. <br>
 
allora la sommatoria verso l'alto (o basso) dei lati <b>pari </b>sarà N^2/8 + N/4 = 2A^2 + A<br>
 
allora la sommatoria verso l'alto (o basso) dei lati <b>pari </b>sarà N^2/8 + N/4 = 2A^2 + A<br>
Line 17: Line 22:
 
ma se A è dispari ==&gt; 2A^2 + A è dispari ==&gt; impossibile perché una sommatoria di numeri pari deve essere per forza pari ==&gt; A deve essere pari ==&gt; N deve essere divisibile per 8
 
ma se A è dispari ==&gt; 2A^2 + A è dispari ==&gt; impossibile perché una sommatoria di numeri pari deve essere per forza pari ==&gt; A deve essere pari ==&gt; N deve essere divisibile per 8
  
−
Alcune considerazioni aggiuntive (che vengono dalla lettura di un articolo congiunto di L. Sallows, M. Gardner, R. Guy e D. Knuth del 1991, <i>Serial Isogons of 90 degrees</i>):<br>
+
Alcune considerazioni aggiuntive (che vengono dalla lettura di un articolo congiunto di L. Sallows, M. Gardner, R. Guy e D. Knuth del 1991, ''Serial Isogons of 90 degrees''):
−
<br>
+
 
 
-Supponiamo, senza perdita di generalita', di cominciare con uno spostamento orizzontale in direzione positiva: affinche' il goligono si chiuda, e' necessario che gli spostamenti orizzontali sommino a zero. E' pero' anche necessario che gli spostamenti ,i&gt;verticali sommino a zero, perche' altrimenti il cammino compiuto non ritornera' mai alla linea del reticolo che passa per l'origine.<br>
 
-Supponiamo, senza perdita di generalita', di cominciare con uno spostamento orizzontale in direzione positiva: affinche' il goligono si chiuda, e' necessario che gli spostamenti orizzontali sommino a zero. E' pero' anche necessario che gli spostamenti ,i&gt;verticali sommino a zero, perche' altrimenti il cammino compiuto non ritornera' mai alla linea del reticolo che passa per l'origine.<br>
−
<br>
+
 
−
- Esiste un modo di mostrare geometricamente che per chiudere un goligono si necessitano di 4<i>n</i> lati, con <i>n</i> eventualmente dispari: se supponiamo di colorare a scacchiera il piano, e senza perdita di generalita' di partire da una casella nera, saremo obbligati (per motivi di parita') a seguire il pattern (se B=casella bianca, N=casella nera) BBNN. Allo stesso modo (l'argomento e' di Gardner -1991- che pero' non lo dimostra) per un N-goligono che si chiude deve essere N=0 (mod 8). Si puo' procedere pensando di porlo su una (quasi)schacchiera fatta cosi'<br>
+
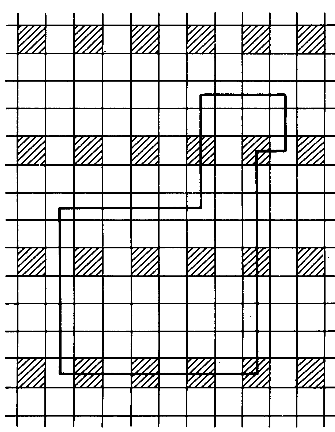
- Esiste un modo di mostrare geometricamente che per chiudere un goligono si necessitano di 4''n'' lati, con ''n'' eventualmente dispari: se supponiamo di colorare a scacchiera il piano, e senza perdita di generalita' di partire da una casella nera, saremo obbligati (per motivi di parita') a seguire il pattern (se B=casella bianca, N=casella nera) BBNN. Allo stesso modo (l'argomento e' di Gardner -1991- che pero' non lo dimostra) per un N-goligono che si chiude deve essere N=0 (mod 8). Si puo' procedere pensando di porlo su una (quasi)schacchiera fatta cosi'
−
<img src="http://img696.imageshack.us/img696/5320/schermata2q.png" alt="" title=""><br>
+
 
−
<br>
+
[[File:Schermata2q.png]]
 +
 
 +
 
 
-Si puo' mostrare che la condizione di congruita' N = 0 (mod 8) e' necessaria e anche <i>sufficiente</i>: per esempio, disponiamo i numeri da 1 a 16 su una riga<br>
 
-Si puo' mostrare che la condizione di congruita' N = 0 (mod 8) e' necessaria e anche <i>sufficiente</i>: per esempio, disponiamo i numeri da 1 a 16 su una riga<br>
 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16<br>
 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16<br>
Line 31: Line 38:
 
+1+2-3-4 5 6 7 8 9 10 11 12-13-14+15+16<br>
 
+1+2-3-4 5 6 7 8 9 10 11 12-13-14+15+16<br>
 
<br>
 
<br>
−
Procediamo cosi' fino a "saturare" tutti i 16 termini di questa sommatoria: fa zero! E non solo, per costruzione sia la somma ristretta ai pari segnati, che quella ristretta ai dispari segnati fa zero. Si usa, in breve, un risultato aritmetico che invito i piu' geek a scrivere e dimostrare:<br>
+
Procediamo cosi' fino a "saturare" tutti i 16 termini di questa sommatoria: fa zero! E non solo, per costruzione sia la somma ristretta ai pari segnati, che quella ristretta ai dispari segnati fa zero. Si usa, in breve, un risultato aritmetico che invito i piu' geek a scrivere e dimostrare:
−
<br>
+
 
−
<img src="http://latex.codecogs.com/gif.latex?%5Cbg_black%20%5C120dpi%20%7B%5Ccolor%7Bwhite%7D%20%5Csum_%7Bk=1%7D%5E%7BN%7D%28-1%29%5E%7B%5Clfloor%20%5Cfrac%7Bk-1%7D%7B2%7D%5Crfloor%7D=0%20%5Ciff%20N%5Cequiv%200%5Cpmod%7B4%7D%7D"><br>
+
<m>\sum_{k=1}^N (-1)^{\lfloor \frac{k-1}{2}\rfloor}k =0 \iff N\equiv 0\pmod{4}</m>
−
<br>
+
 
−
Chiaramente cosi' si generano solo una parte dei goligoni possibili, ma hey, e' gia' qualcosa.<br>
+
Chiaramente cosi' si generano solo una parte dei goligoni possibili, ma hey, e' gia' qualcosa.
−
<br>
+
 
 
- A chi non bastasse pero' si puo' dire all'orecchio che esiste una formula garantita al limone per produrre un goligono "come vogliamo noi" dato un qualunque N=8n. Provare per credere, mettete gli N numeri in fila come sopra, date segno "+" ai primi 2n e agli ultimi 2n numeri, segno - a quelli in mezzo e... la somma e' zero. Provate voi a riscriverlo e a trovare una legge generale: a me non piace molto e l'euristica dopo pranzo non mi sconfinfera.
 
- A chi non bastasse pero' si puo' dire all'orecchio che esiste una formula garantita al limone per produrre un goligono "come vogliamo noi" dato un qualunque N=8n. Provare per credere, mettete gli N numeri in fila come sopra, date segno "+" ai primi 2n e agli ultimi 2n numeri, segno - a quelli in mezzo e... la somma e' zero. Provate voi a riscriverlo e a trovare una legge generale: a me non piace molto e l'euristica dopo pranzo non mi sconfinfera.
  
−
===Verifica di autointersecazione===
+
==Verifica di autointersecazione==
 
si considerano tutte le combinazioni [ {vertice i, vertice i+1} ; {vertice j, vertice j+1} ] con i, i+1 vertici dei lati orizzontali e j, j+1 vertici dei lati verticali e si verifica se:<br>
 
si considerano tutte le combinazioni [ {vertice i, vertice i+1} ; {vertice j, vertice j+1} ] con i, i+1 vertici dei lati orizzontali e j, j+1 vertici dei lati verticali e si verifica se:<br>
−
min(x<sub>i</sub>, x<sub>i+1</sub>) <code>&lt;=</code> x<sub>j</sub> <code>&lt;=</code> max(x<sub>i</sub>, x<sub>i+1</sub>)<br>
+
<m>\big(\min \{x_i,x_{i+1}\} \le x_j \le \max\{x_i, x_{i+1}\}\big)\land\big( \min \{y_j,y_{j+1}\} \le y_i \le \max\{y_j, y_{j+1}\}\big)</m>
−
&amp;<br>
+
 
−
min(y<sub>j</sub>, y<sub>j+1</sub>) <code>&lt;=</code> y<sub>i</sub> <code>&lt;=</code> max(y<sub>j</sub>, y<sub>j+1</sub>)<br>
+
 
Se si verifica è autointersecante.
 
Se si verifica è autointersecante.
  
 
Nb non ho la dimostrazione ma è possibile che si intersechino solo i lati tali che j>i+5 OR i>j+5 (mi pare)
 
Nb non ho la dimostrazione ma è possibile che si intersechino solo i lati tali che j>i+5 OR i>j+5 (mi pare)
  
−
Number of serial isogons of order 8n (or Golygons).
+
==Number of serial isogons of order 8n (or Golygons).==
 
1, 28, 2108, 227322, 30276740, 4541771016, 739092675672, 127674038970623, 23085759901610016, 4327973308197103600, 835531767841066680300, 165266721954751746697155, 33364181616540879268092840
 
1, 28, 2108, 227322, 30276740, 4541771016, 739092675672, 127674038970623, 23085759901610016, 4327973308197103600, 835531767841066680300, 165266721954751746697155, 33364181616540879268092840
  
−
<img src="http://img299.imageshack.us/img299/5882/goly1.png" alt="esatto, non chiavo" title="esatto, non chiavo">
+
==References==
 +
 
 +
* {{en|Golygons}} on en.wikipedia
  
−
REFERENCES
+
* [http://mathworld.wolfram.com/Golygon.html MathWorld page on golygons] (notice that it excludes intersecating golygons)
  
−
L. Sallows, M. Gardner, R. K. Guy and D. E. Knuth, Serial isogons of 90 degrees, Math. Mag. 64 (1991), 315-324.
+
* L. Sallows, M. Gardner, R. K. Guy and D. E. Knuth, ''Serial isogons of 90 degrees'', Math. Mag. 64 (1991), 315-324.
  
−
N. J. A. Sloane and Simon Plouffe, The Encyclopedia of Integer Sequences, Academic Press, 1995 (includes this sequence).
+
* N. J. A. Sloane and Simon Plouffe, ''The Encyclopedia of Integer Sequences'', Academic Press, 1995 (includes this sequence).
  
 
[[Category:Mathematics]]
 
[[Category:Mathematics]]

Latest revision as of 16:20, 31 October 2010

Cube-tamia.jpg
 This page is still incomplete! Please look for updates.


Italian flag.gif
 This page is in Italian. Please help translating it in English.


Golygons of first (N=8) and second (N=16) order.

MANCA UN SACCO DI ROBA ED E' TUTTO UN DISORDINE SIGNORA MIA

per semplificare la questione ed evitare simmetrie, rotazioni e rotture di cazzo il primo lato di lunghezza 1 sarà orientato orizzontalmente verso dx

dato un generico goligono di N lati:
- la sommatoria dei lati dispari sarà <m>\frac{N^2}{4}</m>
- la sommatoria dei lati pari sarà <m>\frac{N^2}{4} + \frac{N}{2}</m>
affinché il goligono sia chiuso:
- i lati dispari che vanno a dx devono avere sommatoria uguale a quelli che vanno a sinistra, pari a <m>\frac{N^2}{8}</m>
- i lati pari che vanno in alto devono avere sommatoria uguale a quelli che vanno in basso, pari a <m>\frac{N^2}{8}+\frac{N}{4}</m>

Dimostrazione che i goligoni devono necessariamente avere numero di lati multiplo di 8

- i lati pari che vanno in alto devono avere sommatoria uguale a quelli che vanno in basso, pari a N^2/8 + N/4</blockquote>ipotizziamo per assurdo che N sia multiplo di 4 ma non di 8, allora può essere scritto nella forma N = 4A dove A è un intero dispari.
allora la sommatoria verso l'alto (o basso) dei lati pari sarà N^2/8 + N/4 = 2A^2 + A

ma se A è dispari ==> 2A^2 + A è dispari ==> impossibile perché una sommatoria di numeri pari deve essere per forza pari ==> A deve essere pari ==> N deve essere divisibile per 8

Alcune considerazioni aggiuntive (che vengono dalla lettura di un articolo congiunto di L. Sallows, M. Gardner, R. Guy e D. Knuth del 1991, Serial Isogons of 90 degrees):

-Supponiamo, senza perdita di generalita', di cominciare con uno spostamento orizzontale in direzione positiva: affinche' il goligono si chiuda, e' necessario che gli spostamenti orizzontali sommino a zero. E' pero' anche necessario che gli spostamenti ,i>verticali sommino a zero, perche' altrimenti il cammino compiuto non ritornera' mai alla linea del reticolo che passa per l'origine.

- Esiste un modo di mostrare geometricamente che per chiudere un goligono si necessitano di 4n lati, con n eventualmente dispari: se supponiamo di colorare a scacchiera il piano, e senza perdita di generalita' di partire da una casella nera, saremo obbligati (per motivi di parita') a seguire il pattern (se B=casella bianca, N=casella nera) BBNN. Allo stesso modo (l'argomento e' di Gardner -1991- che pero' non lo dimostra) per un N-goligono che si chiude deve essere N=0 (mod 8). Si puo' procedere pensando di porlo su una (quasi)schacchiera fatta cosi'

Schermata2q.png


-Si puo' mostrare che la condizione di congruita' N = 0 (mod 8) e' necessaria e anche sufficiente: per esempio, disponiamo i numeri da 1 a 16 su una riga
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
poniamo due segni "+" all'inizio e alla fine:
+1+2 3 4 5 6 7 8 9 10 11 12 13 14+15+16
poniamo due segni meno all'inizio e alla fine:
+1+2-3-4 5 6 7 8 9 10 11 12-13-14+15+16

Procediamo cosi' fino a "saturare" tutti i 16 termini di questa sommatoria: fa zero! E non solo, per costruzione sia la somma ristretta ai pari segnati, che quella ristretta ai dispari segnati fa zero. Si usa, in breve, un risultato aritmetico che invito i piu' geek a scrivere e dimostrare:

<m>\sum_{k=1}^N (-1)^{\lfloor \frac{k-1}{2}\rfloor}k =0 \iff N\equiv 0\pmod{4}</m>

Chiaramente cosi' si generano solo una parte dei goligoni possibili, ma hey, e' gia' qualcosa.

- A chi non bastasse pero' si puo' dire all'orecchio che esiste una formula garantita al limone per produrre un goligono "come vogliamo noi" dato un qualunque N=8n. Provare per credere, mettete gli N numeri in fila come sopra, date segno "+" ai primi 2n e agli ultimi 2n numeri, segno - a quelli in mezzo e... la somma e' zero. Provate voi a riscriverlo e a trovare una legge generale: a me non piace molto e l'euristica dopo pranzo non mi sconfinfera.

Verifica di autointersecazione

si considerano tutte le combinazioni [ {vertice i, vertice i+1} ; {vertice j, vertice j+1} ] con i, i+1 vertici dei lati orizzontali e j, j+1 vertici dei lati verticali e si verifica se:
<m>\big(\min \{x_i,x_{i+1}\} \le x_j \le \max\{x_i, x_{i+1}\}\big)\land\big( \min \{y_j,y_{j+1}\} \le y_i \le \max\{y_j, y_{j+1}\}\big)</m>

Se si verifica è autointersecante.

Nb non ho la dimostrazione ma è possibile che si intersechino solo i lati tali che j>i+5 OR i>j+5 (mi pare)

Number of serial isogons of order 8n (or Golygons).

1, 28, 2108, 227322, 30276740, 4541771016, 739092675672, 127674038970623, 23085759901610016, 4327973308197103600, 835531767841066680300, 165266721954751746697155, 33364181616540879268092840

References

  • L. Sallows, M. Gardner, R. K. Guy and D. E. Knuth, Serial isogons of 90 degrees, Math. Mag. 64 (1991), 315-324.
  • N. J. A. Sloane and Simon Plouffe, The Encyclopedia of Integer Sequences, Academic Press, 1995 (includes this sequence).
Retrieved from "http://wiki.devicerandom.org/index.php?title=Golygons&oldid=253"